上一篇介绍了梯度下降法,对于一些浅层的神经网络来说,可以很容易看到效果,因为每一次迭代,我们都可以将误差降低。而对于深层次的神经网络来说,容易出现一个问题,那就是梯度消失以及梯度爆炸。
来看看这两个问题是怎么产生的。
以下内容参考了哈工大翻译的神经网络教程:
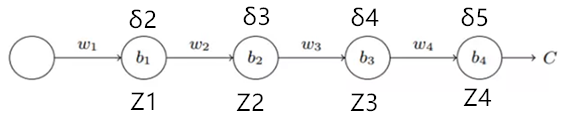
为了弄清楚为何会出现消失的梯度,来看看一个极简单的深度神经网络:每一层都只有一个单一的神经元。下图就是有三层隐藏层的神经网络:
这里,![]() 是权重,而
是权重,而 ![]() 是偏置,
是偏置,![]() 则是某个代价函数。第
则是某个代价函数。第![]() 个神经元的输出 ,其中
个神经元的输出 ,其中![]() 是激活函数,
是激活函数,![]() 是神经元的带权输入,
是神经元的带权输入,![]() 为对应节点的残差。
为对应节点的残差。
为了揭示梯度消失和梯度爆炸的问题,我们计算![]() ,看看会发生什么。
,看看会发生什么。
接下来是计算过程。
结合上一篇文章【从梯度下降到反向传播(附计算例子)】的式子(4)、(6):
![]()
![Rendered by QuickLaTeX.com \[ \delta _{i}^{(l)} = (\sum_{j=1}^{s_{l+1}}W_{ji}^{(l)}\delta_{j}^{(l+1)})\cdot {f}'(z_{i}^{(l)})\qquad(6) \]](https://www.lookfor404.com/wp-content/ql-cache/quicklatex.com-06d0981dd38299ad4ef1923fa4d48e99_l3.png)
式子(4)里面的![]() ,也就是我们上面所说的代价函数
,也就是我们上面所说的代价函数![]() 。
。
由式子(4),可以得到:
![]()
由式子(6),继续进行迭代计算
![Rendered by QuickLaTeX.com \[ \begin{aligned} \frac{\partial C}{\partial b_1}&=\delta_2\\ &={f}'(z_1)w_2\delta_3\\ &={f}'(z_1)w_2{f}'(z_2)w_3\delta_4\\ &={f}'(z_1)w_2{f}'(z_2)w_3{f}'(z_3)w_4\delta_5 \end{aligned} \]](https://www.lookfor404.com/wp-content/ql-cache/quicklatex.com-f444a52a4b607571fc23dc2e70eda8ec_l3.png)
最后的![]() ,就是最后一个节点的残差,由链式求导法则可知:
,就是最后一个节点的残差,由链式求导法则可知:
![]()
代入上式,得到最终结果:
![]()
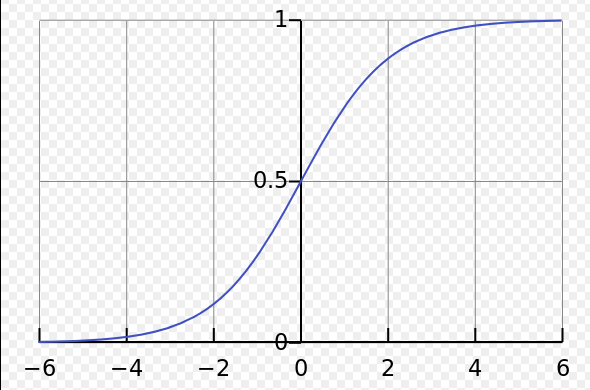
除了最后一项,该表达式是一系列形如![]() 的乘积,我们假设,这里的激活函数f用的是sigmoid函数,sigmoid的图像如下:
的乘积,我们假设,这里的激活函数f用的是sigmoid函数,sigmoid的图像如下:
我们关注的是它的导数,其导数的图像为:
该导数在![]() 时达到最高。现在,如果我们使用标准方法来初始化网络中的权重,那么会使用一个均值0标准差为1的高斯分布。因此所有的权重通常会满足
时达到最高。现在,如果我们使用标准方法来初始化网络中的权重,那么会使用一个均值0标准差为1的高斯分布。因此所有的权重通常会满足![]() 。有了这些信息,我们发现会有
。有了这些信息,我们发现会有![]() 。并且在我们进行了所有这些项的乘积时,最终结果肯定会指数级下降:项越多,乘积的下降的越快。 这,就是梯度消失出现的原因。 同样的,如果我们选择不同的权重初始化方法、以及不同的激活函数,我们也有可能得到
。并且在我们进行了所有这些项的乘积时,最终结果肯定会指数级下降:项越多,乘积的下降的越快。 这,就是梯度消失出现的原因。 同样的,如果我们选择不同的权重初始化方法、以及不同的激活函数,我们也有可能得到![]() 的结果,经过多层累乘,梯度会迅速增长,造成梯度爆炸。
的结果,经过多层累乘,梯度会迅速增长,造成梯度爆炸。
因此,不稳定的梯度问题(梯度消失和梯度爆炸)产生的原因是:在前面的层上的梯度是来自后面的层上项的乘积。
当存在过多的层次时,就出现了内在本质上的不稳定场景。唯一让所有层都接近相同的学习速度的方式是所有这些项的乘积都能得到一种平衡。如果没有某种机制或者更加本质的保证来达成平衡,那网络就很容易不稳定了。简而言之,真实的问题就是神经网络受限于不稳定梯度的问题。所以,如果我们使用标准的基于梯度的学习算法,在网络中的不同层会出现按照不同学习速度学习的情况。
为了解决这个问题,有很多的策略,比如,nlp领域常用的lstm模型,能够解决梯度消失的问题。之后会继续介绍。

![Rendered by QuickLaTeX.com \[\delta _{i}^{(l)} = (\sum_{j=1}^{s_{l+1}}W_{ji}^{(l)}\delta_{j}^{(l+1)})\cdot {f}'(z_{i}^{(l)})\qquad(6) \]](https://www.lookfor404.com/wp-content/ql-cache/quicklatex.com-32421dd455d9b10085d3f94ebf64fb10_l3.png)
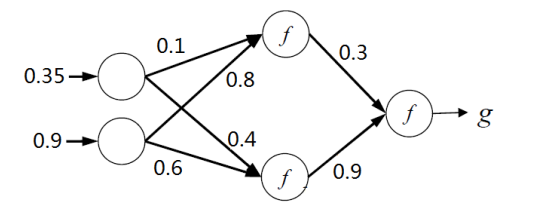
![Rendered by QuickLaTeX.com \[ \delta _{1}^{(2)} = (\sum_{j=1}^{1}W_{j1}^{(2)}\delta_{j}^{(3)})\cdot {f}'(z_{1}^{(2)})\\ =W_{11}^{(2)}\delta_{1}^{(3)}\cdot {f}'(z_{1}^{(2)})\\ =0.3\cdot0.3385\cdot1\\ =0.10155 \]](https://www.lookfor404.com/wp-content/ql-cache/quicklatex.com-7647c8d5bd7a8efa592c58f679e6bd80_l3.png)
![Rendered by QuickLaTeX.com \[ \delta _{2}^{(2)} = (\sum_{j=1}^{1}W_{j2}^{(2)}\delta_{j}^{(3)})\cdot {f}'(z_{2}^{(2)})\\ =W_{12}^{(2)}\delta_{1}^{(3)}\cdot {f}'(z_{2}^{(2)})\\ =0.9\cdot0.3385\cdot1\\ =0.30465\\ \]](https://www.lookfor404.com/wp-content/ql-cache/quicklatex.com-df1409e3e80e96c51cea504bddaa0af2_l3.png)
![Rendered by QuickLaTeX.com \[ \delta _{1}^{(1)} = (\sum_{j=1}^{2}W_{j1}^{(1)}\delta_{j}^{(2)})\cdot {f}'(z_{1}^{(1)})\\ =(W_{11}^{(1)}\delta_{1}^{(2)}+W_{21}^{(1)}\delta_{2}^{(2)})\cdot {f}'(z_{1}^{(1)})\\ =(0.1\cdot0.10155+0.4\cdot0.30465)\cdot1\\ =0.132015 \]](https://www.lookfor404.com/wp-content/ql-cache/quicklatex.com-cdf602de8338d4aaec76cc6627d7e16c_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{aligned} output &= a_{1}^3\\ &={f}(z_{1}^3)\\ &=f(0.17221625\cdot{f}(z_{1}^2)+0.78491\cdot{f}(z_2^2))\\ &=0.17221625\cdot{z}_{1}^2+0.78491\cdot{z}_2^2\\ &=0.17221625\cdot(0.35\cdot 0.08222875+0.9\cdot 0.7543025)\\&+0.78491\cdot(0.35\cdot0.34668625+0.9\cdot0.4629075)\\ &\approx 0.1219 + 0.4222\\ &=0.5441 \end{aligned} \]](https://www.lookfor404.com/wp-content/ql-cache/quicklatex.com-b99a065e289ab2b16778ea8078742e22_l3.png)