从梯度下降到反向传播(附计算例子)

梯度下降法（Gradient Descent）是神经网络的核心方法，用于更新神经元之间的权重，以及每一层的偏置；反向传播算法（Back-Propagation Algorithm）则是一种快速计算梯度的算法，从而能够使得梯度下降法得到有效的应用。

以前刚开始看神经网络的教程，一堆数学的公式、字母，看得头发昏。这学期上了模式分类的课，老师的ppt里面有计算的例子，随手算一算这些例子，再回过头去理解梯度下降和反向传播，就很容易了。所以今天我将结合具体的计算例子来谈谈它们。

在以下内容进行之前，你最好对神经网络里面的各个参数有个了解，特别是关于权重W的表达方式，不然下标容易搞混，具体可以参看【ufldl的神经网络教程】

先来直观的感受下这两个概念在神经网络里面的地位。

梯度下降法

所谓梯度，就是指向标量场增长最快的方向。

对于一个神经网络而言，我们的目标是为了找到最适合的权重，使得最终的输出和我们预期的输出相差不大，也就是说，问题可以转化为，找到适当的权重值，使得最终误差最小。而为了使得最终误差最小，我们就得利用梯度下降法，对连接每一个神经元的边的权重进行迭代更新，更新后的权重构成的神经网络，误差变小，多次迭代，直到我们满意（误差小于一个阈值）。

反向传播算法

利用梯度下降法，每次更新权重如下：

$W_{ij}^l=W_{ij}^{l}-\alpha \frac{\partial J(W,b)}{\partial W_{ij}^{l}}\qquad (1)$

$b_{i}=b_{i}^{l}-\alpha \frac{\partial J(W,b)}{\partial b_{i}^{l}}\qquad (2)$

其中，α为学习率， $J(W,b)$ 是我们定义的损失函数，通常是 $J(W,b)=\frac{1}{2}\left \| output - y \right \|^2$ ，output为我们使用当前的权重计算出来的输出，y为训练数据的输出，用这个函数可以度量损失、误差。

从上面的式子可以知道，我们只要对每条边Wij计算出对应的 $\frac{\partial J(W,b)}{\partial W_{ij}^{l}}$ ，以及对每个偏置bi计算出对应的 $\frac{\partial J(W,b)}{\partial b_{i}^{l}}$ ，就可以对权重和偏置进行更新了。

反向传播算法，就是用来计算 $\frac{\partial J(W,b)}{\partial W_{ij}^{l}}$ 和 $\frac{\partial J(W,b)}{\partial b_{i}^{l}}$ 的。完整的反向传播算法可以看这里，无非就是链式求导法则的应用，别被公式吓到了。下面的式子，就不给出推导过程了。

在反向传播算法里面，我们定义一个残差的概念，每一个节点都有一个残差，我们用 $\delta _{i}^{(n_{l})}$ 表示第nl层，的第i个节点的残差，它的计算公式如下：

$\frac{\partial J(W,b)}{\partial z_{i}^{(n_{l})}}$

其中的 $z_{i}^{(n_{l})}$ ，是nl-1层网络对第nl层，第i个节点的输入和。

有了残差的这个概念，我们计算 $\frac{\partial J(W,b)}{\partial W_{ij}^{l}}$ 和 $\frac{\partial J(W,b)}{\partial b_{i}^{l}}$ 就很方便了，经过链式求导法则的推导，我们最终可以得到以下计算公式：

$\frac{\partial J(W,b)}{\partial W_{ij}^{l}}=a_{j}^{(l)}\delta _{i}^{(l+1)}\qquad(3)$

$\frac{\partial J(W,b)}{\partial b_{i}^{l}}=\delta _{i}^{(l+1)}\qquad(4)$

其中， $a_{j}^{(l)})$ 是使用当前权重和偏置前向计算得出的第l层、第j个输出值。

在这里停一下，我们把问题捋一捋。现在问题就转化为，只要我们能够计算到每一个节点的残差值 $\delta _{i}^{(n_{l})}$ ，那么根据（3）和（4），我们就可以计算出每一个 $\frac{\partial J(W,b)}{\partial W_{ij}^{l}}$ 和 $\frac{\partial J(W,b)}{\partial b_{i}^{l}}$ ，有了它们，就可以用（3）和（4）更新权重了。

所以，问题就转化为了求每一个节点的残差。以下的（5）、（6）两个式子，就解释了反向传播算法为什么要叫做反向传播算法。先直接给出公式。

对于最后一层输出层，残差为：

$\delta _{i}^{(n_{l})} = -(y_{i}-a_{i}^{(n_{l})})\cdot {f}'(z_{i}^{(nl)})\qquad(5)$

其中 $y_{i}$ 是训练样本（x,y）的第i个输出值， $a_{i}^{(n_{l})})$ 是使用当前权重和偏置前向计算得出的第l层（也就是这种情况下所说的输出层）、第i个输出值， $z_{i}^{(nl)}$ 则是nl-1层网络对第nl层，第i个节点的输入和。

有了最后一层各个节点的残差值，就可以利用它们计算前一层各个节点的残差值了，这也就是反向传播算法的精髓所在，计算公式如下：

$\delta _{i}^{(l)} = (\sum_{j=1}^{s_{l+1}}W_{ji}^{(l)}\delta_{j}^{(l+1)})\cdot {f}'(z_{i}^{(l)})\qquad(6)$

式子（6）看上去有点复杂，我直接用文字描述一下：第l层的第i个节点A的残差=【【第l+1层所有和A有连接的节点的残差】乘以对应连接权重，最后求和】乘以节点A的激活函数的导数。

似乎越描越黑。没关系，最后，来个计算的例子，就会明白了。

反向传播算法计算例子

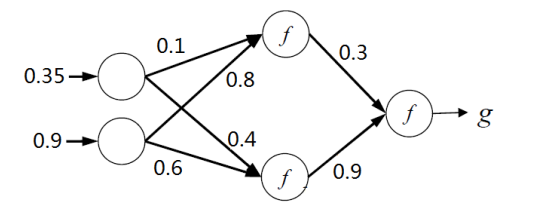
给出如下一个三层的神经网络（为了演绎计算过程，这个神经网络没有设置偏置b，如遇到有偏置的情况，也可以利用以上（1）-（6）的公式计算，是类似的。），并且假设f（a）=a（即这个函数的导数是1），损失函数为 $J(W,b)=\frac{1}{2}\left \| output - y \right \|^2$ ，目标值为0.5，学习率α=0.5：

我们来演绎一下，如何利用反向传播算法来更新权重。

首先用前向传播计算出每一个节点的值：

$z_{1}^{2} = 0.35 \cdot 0.1 + 0.9 \cdot 0.8 = 0.755$

$a_{1}^{2} = {f}(z_{1}^{2}) = 0.755$

$z_{2}^{2} = 0.35 \cdot 0.4 + 0.9 \cdot 0.6 = 0.68$

$a_{2}^{2} = {f}(z_{2}^{2}) = 0.68$

$z_{1}^{3} = 0.3 \cdot 0.755 + 0.9 \cdot 0.68 = 0.8385$

$a_{1}^{3} = {f}(z_{1}^{3}) = 0.8385\qquad (7)$

计算这5个节点的残差（事实上第一层的残差不需要计算，我们也可以得到结果了，但为了演绎公式，我下面还是进行了计算）。

先从最后一个节点（输出节点）开始，由式子（5），得：

$\delta _{1}^{(n_3)} = -(y_{1}-a_{1}^{(3)})\cdot {f}'(z_{1}^{(n3)}) \\ = -(0.5-0.8385)\cdot 1 = 0.3385 \\$

然后是倒数第二层，由式子（6），得：

$\delta _{1}^{(2)} = (\sum_{j=1}^{1}W_{j1}^{(2)}\delta_{j}^{(3)})\cdot {f}'(z_{1}^{(2)})\\ =W_{11}^{(2)}\delta_{1}^{(3)}\cdot {f}'(z_{1}^{(2)})\\ =0.3\cdot0.3385\cdot1\\ =0.10155$

$\delta _{2}^{(2)} = (\sum_{j=1}^{1}W_{j2}^{(2)}\delta_{j}^{(3)})\cdot {f}'(z_{2}^{(2)})\\ =W_{12}^{(2)}\delta_{1}^{(3)}\cdot {f}'(z_{2}^{(2)})\\ =0.9\cdot0.3385\cdot1\\ =0.30465\\$

最后是倒数第三层，也就是第一层，其实第一层是不用计算的，但是为了演示公式，这里还是计算一下第一层的第一个节点的残差，第二个节点就不算了。由式子（6），得：

$\delta _{1}^{(1)} = (\sum_{j=1}^{2}W_{j1}^{(1)}\delta_{j}^{(2)})\cdot {f}'(z_{1}^{(1)})\\ =(W_{11}^{(1)}\delta_{1}^{(2)}+W_{21}^{(1)}\delta_{2}^{(2)})\cdot {f}'(z_{1}^{(1)})\\ =(0.1\cdot0.10155+0.4\cdot0.30465)\cdot1\\ =0.132015$

计算好所需要的残差 $\delta _{1}^{(n_3)}$ , $\delta _{1}^{(2)}$ 和 $\delta _{2}^{(2)}$ 之后，我们就可以计算 $\frac{\partial J(W,b)}{\partial W_{ij}^{l}}$ 了。

由式子（3），我们计算所有损失函数对W的偏导：

$\frac{\partial J(W,b)}{\partial W_{11}^{1}}=a_{1}^{(1)}\delta _{1}^{(2)}\\ =0.35\cdot 0.10155\\ =0.0355425$

$\frac{\partial J(W,b)}{\partial W_{21}^{1}}=a_{1}^{(1)}\delta _{2}^{(2)}\\ =0.35\cdot 0.30465\\ =0.1066275$

$\frac{\partial J(W,b)}{\partial W_{12}^{1}}=a_{2}^{(1)}\delta _{1}^{(2)}\\ =0.9\cdot 0.10155\\ =0.091395$

$\frac{\partial J(W,b)}{\partial W_{22}^{1}}=a_{2}^{(1)}\delta _{2}^{(2)}\\ =0.9\cdot 0.30465\\ =0.274185$

$\frac{\partial J(W,b)}{\partial W_{11}^{2}}=a_{1}^{(2)}\delta _{1}^{(3)}\\ =0.755\cdot 0.3385\\ =0.2555675$

$\frac{\partial J(W,b)}{\partial W_{12}^{2}}=a_{2}^{(2)}\delta _{1}^{(3)}\\ =0.68\cdot 0.3385\\ =0.23018$

之后，就可以更新权重了。

$W_{11}^1=W_{11}^{1}-\alpha \frac{\partial J(W,b)}{\partial W_{11}^{1}} \\ =0.1 - 0.5\cdot0.0355425\\ =0.08222875$

$W_{21}^1=W_{21}^{1}-\alpha \frac{\partial J(W,b)}{\partial W_{21}^{1}} \\ =0.4 - 0.5\cdot0.1066275\\ =0.34668625$

$W_{12}^1=W_{12}^{1}-\alpha \frac{\partial J(W,b)}{\partial W_{12}^{1}} \\ =0.8 - 0.5\cdot0.091395\\ =0.7543025$

$W_{22}^1=W_{22}^{1}-\alpha \frac{\partial J(W,b)}{\partial W_{22}^{1}} \\ =0.6 - 0.5\cdot0.274185\\ =0.4629075$

$W_{11}^2=W_{11}^{2}-\alpha \frac{\partial J(W,b)}{\partial W_{11}^{2}} \\ =0.3 - 0.5\cdot0.2555675\\ =0.17221625$

$W_{12}^2=W_{12}^{2}-\alpha \frac{\partial J(W,b)}{\partial W_{12}^{2}} \\ =0.9 - 0.5\cdot0.23018\\ =0.78491$

权重更新完毕，我们来验证一下效果是否有提升：

$\begin{aligned} output &= a_{1}^3\\ &={f}(z_{1}^3)\\ &=f(0.17221625\cdot{f}(z_{1}^2)+0.78491\cdot{f}(z_2^2))\\ &=0.17221625\cdot{z}_{1}^2+0.78491\cdot{z}_2^2\\ &=0.17221625\cdot(0.35\cdot 0.08222875+0.9\cdot 0.7543025)\\&+0.78491\cdot(0.35\cdot0.34668625+0.9\cdot0.4629075)\\ &\approx 0.1219 + 0.4222\\ &=0.5441 \end{aligned}$

目标值是0.5，权重未更新的时候，我们算出输出值为0.8385（计算过程在式子(7)）,现在更新权重过后，算出来的输出值是0.5441，显然效果提升了，之前做的工作是有用的！

从梯度下降到反向传播(附计算例子)

梯度下降法

反向传播算法

反向传播算法计算例子